Math: Memory Challenges
Helping Students with Poor Working Memory
Often an educational evaluation will describe a dyslexic student as having “low working memory.” Low working memory is indicated when someone cannot keep many things on their “screen.” For example, think about when you first learned to drive. You had many steps to remember. You held those steps in your active working memory. Once you drove a lot, you didn’t think about where the key went, where your feet should be positioned, when you needed to look in the mirrors (and know which ones to look at), where to put the shifter, which side the blinkers were on, etc. Multistep problems or directions pose the same challenge for students with low working memory. For instance, when they are borrowing in subtraction they have to hold onto numbers as they work through the problem. Students with low active-working memory usually have to write everything down. They also benefit from underlining/highlighting directions before they start.
Many struggling math students can enhance their memory of processing steps if they name each step of a math process as it is being performed. This strategy requires students (and teachers) to slow down, but the investment of time increases the student’s ultimate grasp and retention of the mathematical concept.
Dyslexics often experience difficulty remembering directions and learning sequences that they hear. This hampers their ability to sequence and plan sequential steps as they may not be able to hold auditory information long enough to process it. In terms of math, a student may be unable to remember elements of word problems long enough to perform an operation. He may know that he needs to subtract one value from another, but he may not be able to keep those numbers in his head long enough to hear the whole word problem. This is not to imply that a low digit span correlates with being dyscalculic; however, auditory-memory limitations will make it difficult to utilize certain math strategies and related procedures.
Woodin uses a combination of logic and visualization strategies, including graphic organizers, to help students who have difficulty formulating and comparing multiplication facts and other mathematical processes. Once internalized, graphic organizers, like a clock face or familiar dot patterns, help students because they can “chunk” a great deal of information into an organized package that they can access and use to orient themselves. Without imposed organization, facts are learned as isolated sentences through rehearsal-like phone numbers. Dyslexics are big-picture thinkers, and being able to organize through context is a helpful strategy.
Woodin:Traditional count-up strategies for subtraction ask students to count up from the subtrahend (smallest number) up to the minuend (larger number). For example, subtracting 12 – 8 would involve saying “eight” and then counting up to 12 while keeping track of the beats of the counting sequence: “. . . nine, ten, eleven, twelve.” Usually this is done using physical expressions, such as points on a number line, plastic counters, or outstretched fingers, to record the number of counts (4). The student responds by saying or writing “four.” If the student is not prompted to repeat the entire fact sentence, he will, for a short time, remember only the disassociated “four” until it fades. Individuals who are able to benefit from this strategy must have the capacity to retain the original fact (12 – 8) prompt after finding the answer, and merge the two pieces of information into a complete fact to store in its entirety. Without this capacity, students must continue to count to find sums and differences, and thus fail to develop their fact base.
When a student is asked to change the order of a sequence, the counting sequence (8, 9, 10, 11) may be familiar in that order; however, subtracting 3 from 11 by counting backward, another traditional strategy, may be difficult. For instance, consider the analogous task of saying the alphabet backward three letters from the letter K. The student must hold the initial K, then repeat a forward sequence that includes it—H, I, J, K—and then hold the sequence in memory as he manipulates the order. The student says “K . . . J . . . I” but cannot remember the letter H that started the sequence. He must start over, give up, or, perhaps write the sequence on paper and track each letter with his pencil point as he counts down to help manage this sequencing task.
Example Strategy I: Writing Problems Out To Free Up Memory
The act of writing the forward sequence on paper (G H I J K) has an immediate benefit. It may now be read in reverse order. In this case the whole sequence of letters (parts) is provided visually in an organized fashion so they may be selected and reordered, one at a time. NOTE: The negative aspect of this process is that the student never sequences the information mentally, and won’t be able to reproduce the linear sequence visually in his mind’s eye. When confronted by a similar problem, he will have to refer to another written model.
Example Strategy II: Chunking Strategies
Woodin: Chunking strategies can be used effectively. The ability to recognize a number of briefly presented items without actually counting is called subitizing (from lat. subito= suddenly). Adult subjects can predictably subitize 1 to 4 randomly placed items. Larger quantities of dots or objects greater than five are either counted or partitioned into smaller, recognizable “chunks” and added. If larger quantities are presented in predictable patterns, these patterns can be learned so that they too may be instantly recognized or subitized (Wolters et al., 1987. “Quantification of Small Numbers of Dots: Subitizing or Pattern Recognition?” American Journal of Psychology, Summer). The spatial arrangement of sets influences how difficult they are to subitize. Canonical patterns occur on dice and playing cards and dominoes. Canonical patterns, like the x-shaped “quincunx” 5 on a die, are processed substantially faster than random, noncanonical patterns. Furthermore, if a complex pattern can be broken down into small canonical patterns, then participants can follow a partition and add strategy (Wender et. al, 2000).

Young children may be instructed to use perceptual subitizing to build their initial ideas of cardinality by counting small, recognizable groups of things. For example, their first cardinal meanings for number words may be labels for small sets of subitized quantities, even if they determined the labels through counting. Consider counting the first four dots on a number line versus counting the corners of a square. Which method develops a more durable concept of the quantity of four? The gestalt of the square organizes the counting sequence into a single durable unit, comprised of four elements.
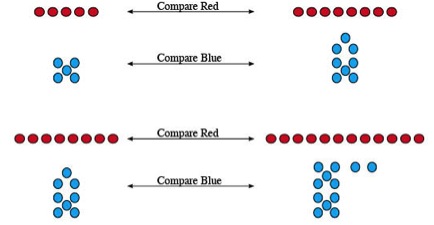
In mathematics, the cardinality of a set is a measure of the “number of elements of the set.” Rather than trying to establish cardinality by counting objects in a linear fashion (from part to whole), consider the benefit realized by counting the elements of a recognized set from whole to part. For instance, instead of counting a handful of cereal, one by one, to determine the quantity: “one, two, three, four, five” (•••••), arrange the five pieces into an identifiable “X” pattern of cereal, say, “This is five.” then proceed to count the five parts. Whole-to-part processing models provide the ability to integrate parts within the context of a whole number to establish cardinality. The illustration above depicts clusters of dots in both linear and iconic patterns. Identify the number of dots in each cluster. Note how easy it is to identify and compare the two blue clusters in contrast to the way that you compare the two red clusters. Note the manner that you use to compare each colored pair, as well as your efficiency. As the quantities increase, consider how the visual patterning streamlines this task by making it easier to identify the quantity of elements and compare them.
About Chris Woodin:
Christopher Woodin is a specialist in the field of mathematics and learning disabilities. A graduate of Middlebury College and Harvard Graduate School of Education, he has taught extensively at Landmark School in Massachusetts. At Landmark School’s Elementary/Middle School Campus, he holds the Ammerman Chair of Mathematics. Christopher served on the Massachusetts Department of Education’s Mathematics 2011 Curriculum Framework Panel, and teaches graduate-level professional development courses during the summer through Landmark’s Outreach Program. Chris was the 1997 Massachusetts Learning Disabilities Association (LDA) Samuel Kirk Educator of the Year. He has presented at numerous international LDA and International Dyslexia Association (IDA) conferences, and has led math workshops to audiences across the country.
Christopher has published The Landmark Method of Teaching Arithmetic ©1995 and several journal articles. His latest project, Multiplication and Division Facts for the Whole-to-Part, Visual Learner: An Activity-Based Guide to Developing Fluency with Math Facts, is currently in press and due to be released in 2012. This comprehensive text features the methodologies and many of the activities that are described on The Yale Center for Dyslexia & Creativity’s website. To learn more about Mr. Woodin and his work, please visit his page on the Landmark School website and his own website.
Related
Math: Processing Breakdowns
Students with slower processing speeds or executive-function problems are often no different from their peers in math proficiency in first and second grade; but as they confront multistep computations in upper elementary school tests, their scores tumble because they lack the skills necessary to produce organized, efficient output.
Read MoreMath: Naming Problems
Math-specific concepts seem to be particularly difficult to master. In addition to being abstract, these concepts contain terms that confound students with visual similarity or auditory similarity between homophones.
Read More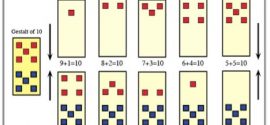
Math: Counting & Comparing
A common response to students who are having counting problems is to simply have them do daily counting practice; however, students with counting and comparing difficulties also benefit from practice that utilizes patterns and relationships.
Read MoreMath Introduction
Since the YCDC website began in 2007, we have received many requests about how best to help dyslexic students struggling with math.
Read More